Annideas?

昨天認識過 Ruby的語彙符號 之後，今天開始來認識Ruby 資料型別中的 數字。

Ruby的數字類別分層結構

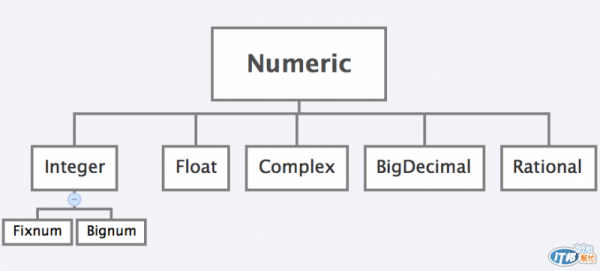
這是書中所給的數字的類別樹狀圖，身為數學系畢業的學生，一連串的問題就在腦中浮現了…

「這數字分類好像跟真實數系不一樣？」

「Numeric 再上一層，也就是他的爸爸、爺爺是誰？」

「Numeric 的兄弟姐妹是誰？」

我是一個需要視覺化學習的人，沒看到整棵樹的全貌，很容易搞不清楚這些樹枝之間的關係與功能。

雖然書上提到Ruby 的數字方法很直觀也不難，但還是想多花點時間先把前置經驗建構起來～

數學的數系

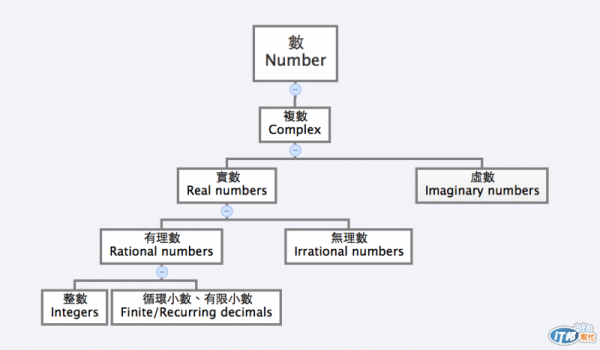
看到這兩張樹狀圖就知道為什麼我會困惑這麼久了吧XD 對我來說Integer 包含於Rational 包含於Complex (換句話說：Integer的爸爸是Rational; Rational 的爺爺是Complex)，怎麼到了Ruby 他們反而被寫在同一層了(大家都是兄弟姐妹)！

所以寫了一些程式碼來讓自己更理解一點，在數的後面加上 .class ，可以知道他是什麼類別！

1.class       => Fixnum      #比較小的整數是Fixnum
3.14159.class => Float       #小數都是浮點數
(3+4i).class  => Complex     #有配個i的都是複數
(3/2).class   => Fixnum      #??????????????????

哈，打到這裡出現兩個疑問，小的整數是Fixnum，那要多大才會變成Bignum 呢？書中只提到儲存於31 位元空間內的整數都是Fixnum，但還是太抽象了，所以我立馬試試到底Fixnum 和Bignum 的分界在哪？就出現了下面這個圖XD

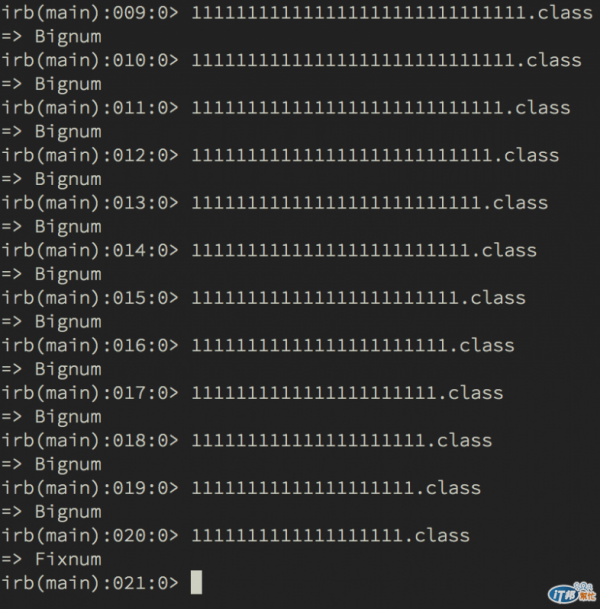
我真的太無聊了XD 不過也因此發現，原來19 位整數是Fixnum，到20 位整數就變成Bignum了！！

另外還有一個問題，3/2 應該有兩種可能，一種是分數、一種是除完以後變成1.5 的小數，但是用Ruby 執行的結果卻是Fixnum ?????????

再仔細翻翻書，就看到了答案，原來…【The Ruby Programming Language】p.46 所述：

『除法運算符取決於運算元所屬類別：如果兩個運算元皆為整數，則會進行截尾整數除法(truncating integer division)運算。如果有一個運算元是一個Float，則會進行浮點數除法運算。』

3/2   => 1      #被截尾了，小數點後全都截光光
3.0/2 => 1.5
3/2.0 => 1.5
1/4   => 0      #被截尾了，小數點後全都截光光
1.0/4 => 0.25
#只要分子或分母出現浮點數，都會按照浮點數的除法運算

這樣可以了解為什麼3/2當時會出現Fixnum 了，因為他的結果是1，所以當然判斷它為Fixnum。

Ruby的算術

接下來提幾個基本的數學除法運算，還記得國小數學老師就有教，除以零是沒有意義的，做答請回答「無意義」，我們看看Ruby 怎麼處理除以零的問題：

0/2   => 0
0.0/2 => 0.0       # 0除以別人都很正常

2/0   ZeroDivisionError: divided by 0 # 整數除以0會出現Error
0/0.0 => NaN       # NaN = Not-a-Number
0.0/0 => NaN       # NaN = Not-a-Number
9.2/0 => Infinity  # 哇9.2除以0有無限大的力量(?)

有點酷，明明都是除以0，卻有三種不同的結果！整數的跟小學老師教的一樣，不可以做沒意義的事，所以出Error，但是另外兩種就很神奇，書中只說0.0/0.0是一個特例，而另外9.2/0有無窮大的的結果(?) 是說書中有提到浮點數除以0是不會報錯的，只會傳回Infinity，很想知道原因，這部分我還需要再查查資料、做做功課才能理解，之後懂了再補上來！

最後再來簡介幾個書中提到的算術例子給大家參考：

2**10       => 1024      # 2的10次方
2**-1       => (1/2)     # 2的-1次方
25**(1/2.0) => 5.0       # 25的1/2次方 = 25的平方根
8**(1/3.0)  => 2.0       # 8的1/3次方 = 8的立方根
4**3**2     => 262144    # 計算順序由右到左，等於4**(3**2) = 4**9

打到這裡突然又想到，所有比20 位還多的整數都是Bignum嗎？沒有範圍嗎？所以做了以下測試：

2**10000000000000000000000000000000000000000
 warning: in a**b, b may be too big
=> Infinity

(2**10000000000000000000000000000000000000000).class
 warning: in a**b, b may be too big
=> Float

當數字太大，系統會跟你警告！這太大了噢！然後跟你說這已經是Infinity 無窮大的數了，這時候檢查他的類別，當他大到無窮大時，他就不是屬於Bignum 的類別，而是Float 浮點數了！酷XD！數字真有趣XD

今天只有介紹完數字，還留下了一些問題Orz，大概自己是數學老師，所以對數學有點偏執吧，這裡的疑惑好像都不是什麼重要的疑惑啊XD"之後會想辦法再弄更清楚的！

If it ain't fun, don't do it.

今天想說，如果這件事不好玩，就不要做了！我繼續寫下去，是因為我覺得這很好玩:D！